Spatial Analysis and Decision Assistance

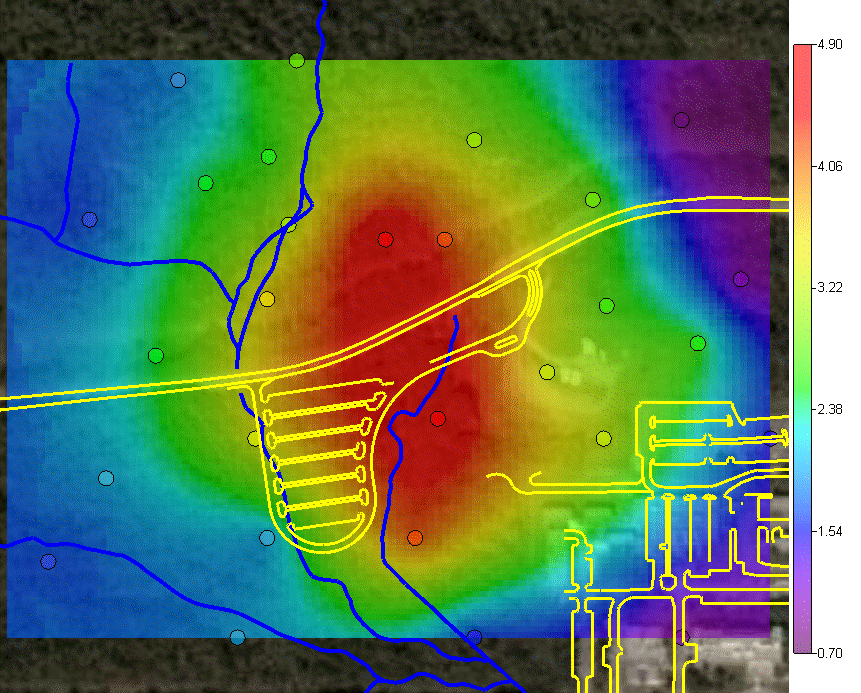
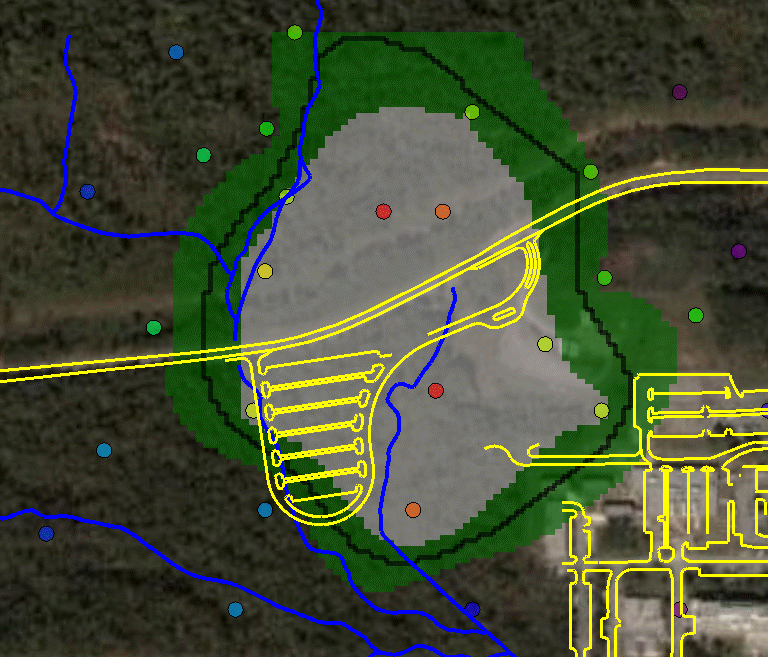
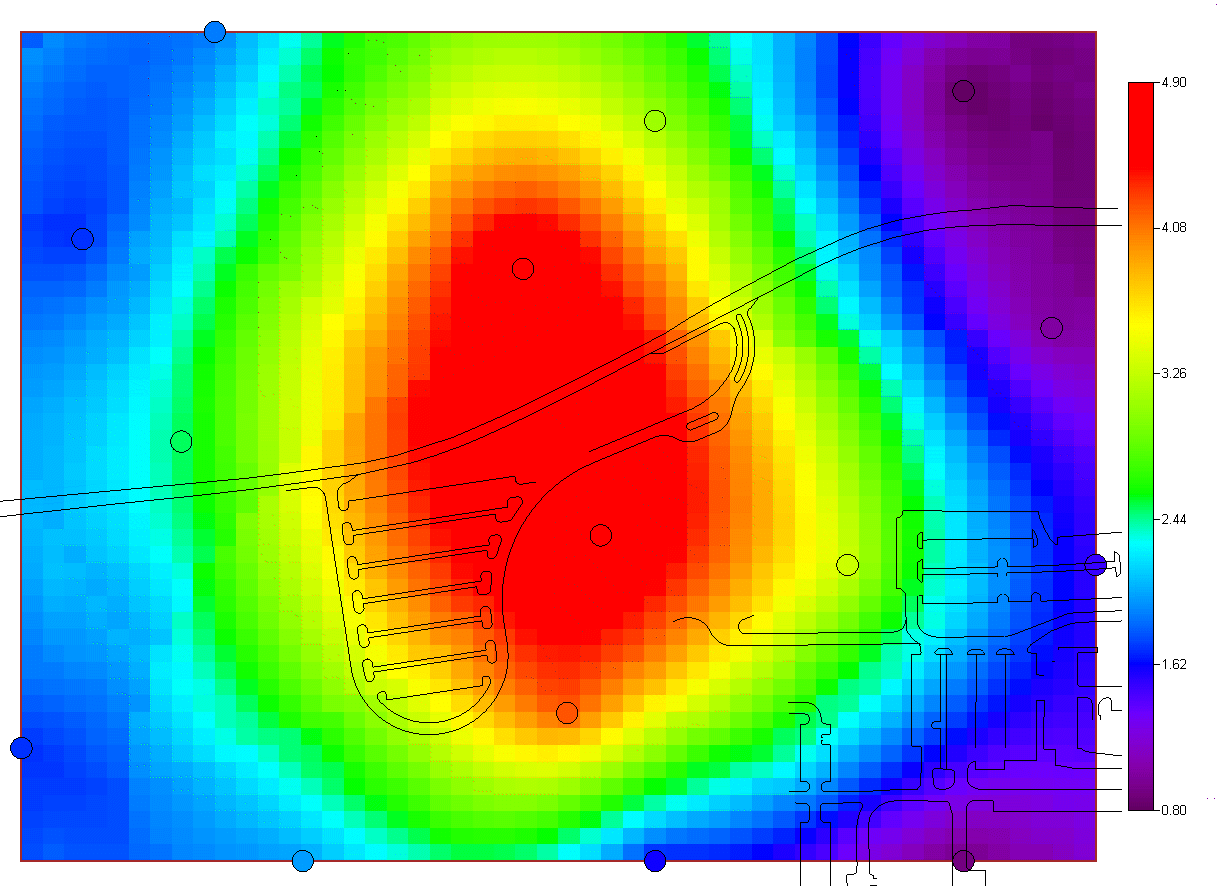
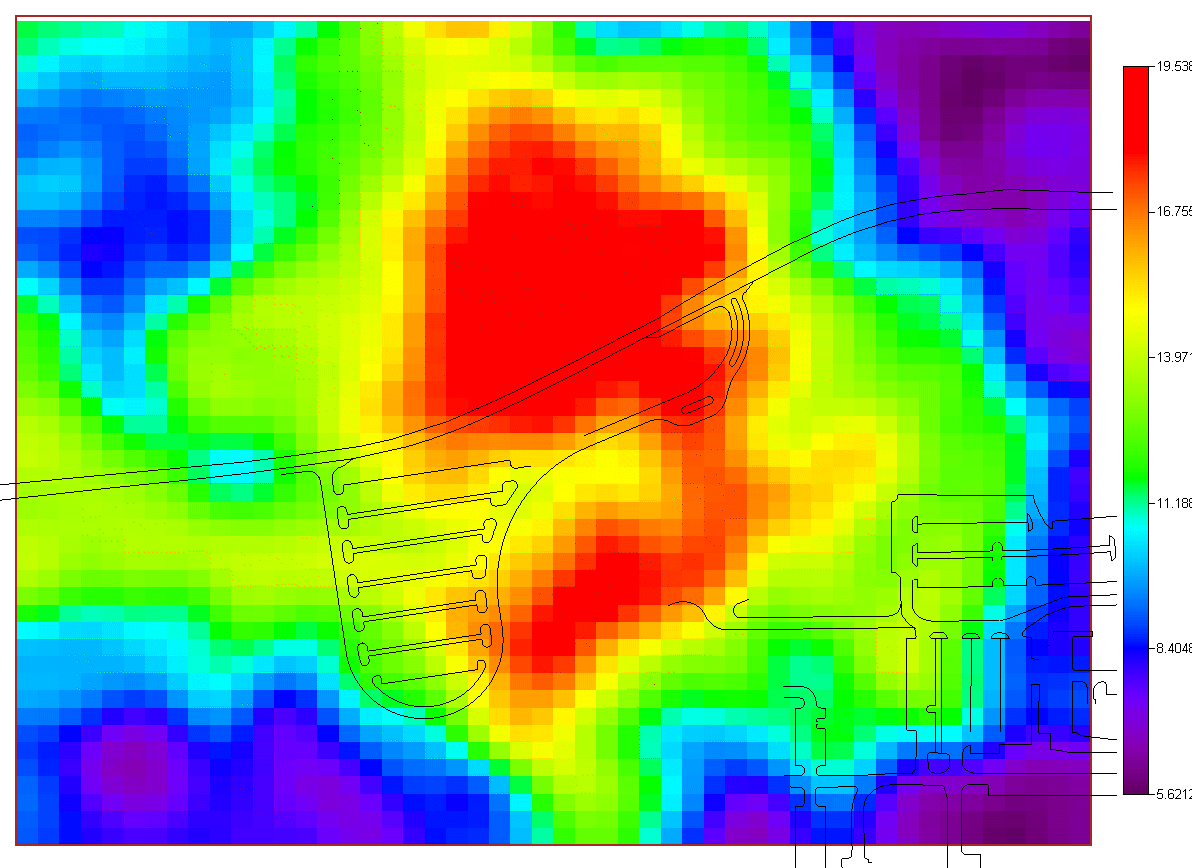
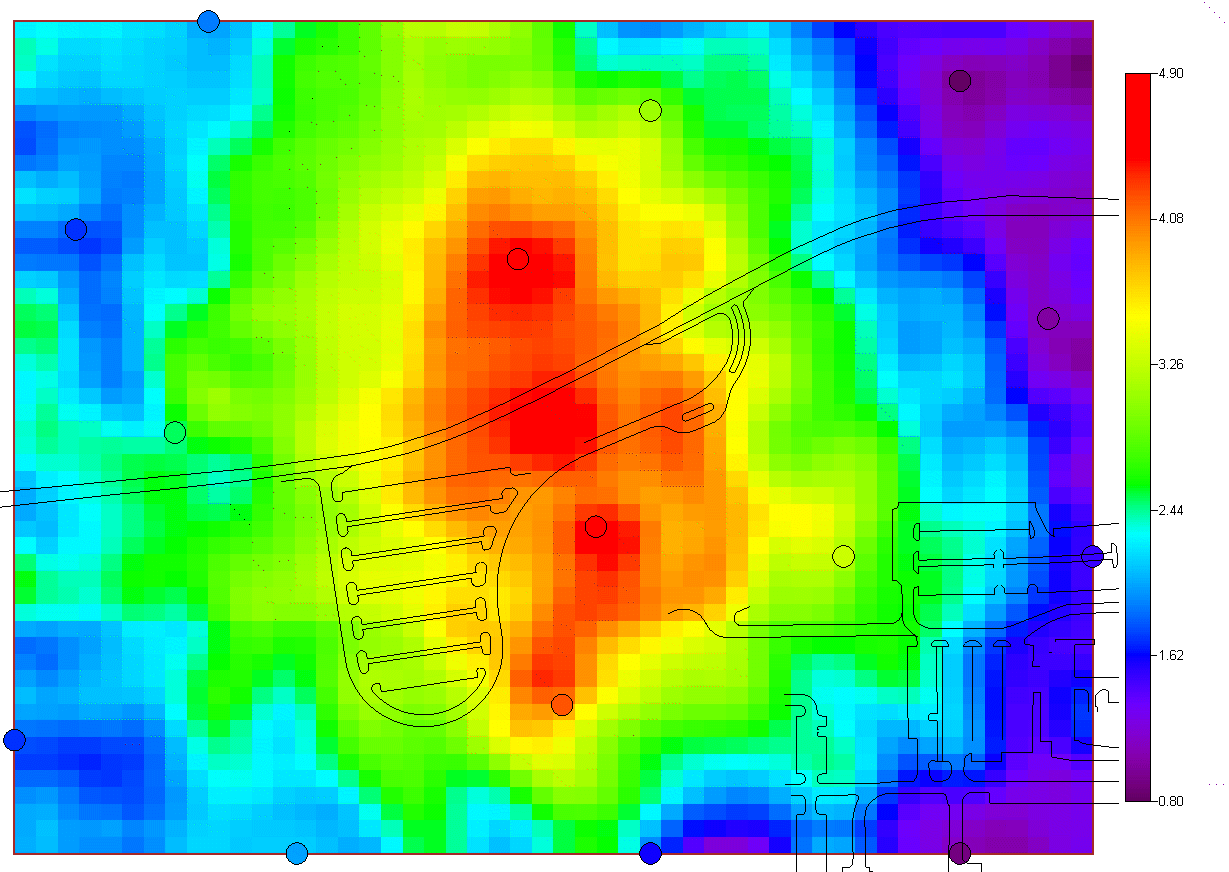
Geospatial Analysis

Several tools are provided in SADA for performing a geospatial analysis. These tools include methods for measuring spatial correlation among data, modeling spatial correlation, and producing concentration, risk, probability, variance, and cleanup maps. Among these tools includue seven options:

ordinary kriging,
indicator kriging,
cokriging
inverse distance,
natural neighbor,
nearest neighbor.
import your own

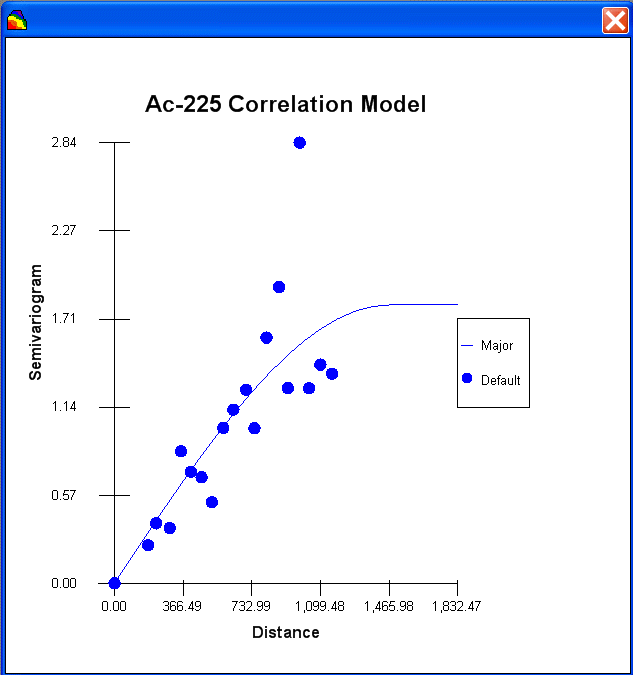
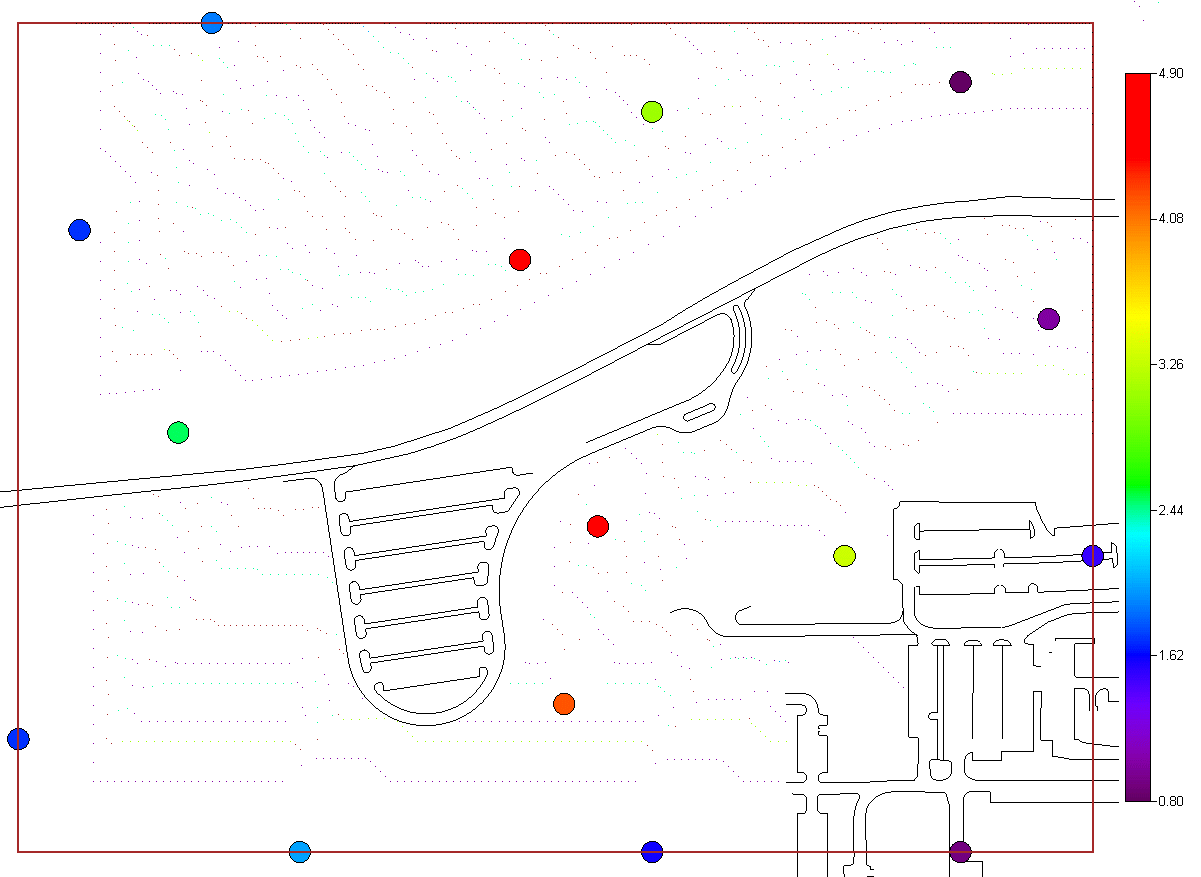
and two simulation methods.

The last option "import your own" may be of particular interest. SADA has a couple of industry standard formats (ASCII Grid, FLOAT Grid) as well as a SADA format (fairly low requirements for importing 3d models) for importing your own models. When you import your own models, they can be used in line with the other modeling and decision analysis features just as if they were generated in SADA.

Basic estimation methods such as inverse distance, natural neighbor, and nearest neighbor produce a single estimation map for a given set of model parameters. Natural neighbor is particularly easy for novice users as it requires no input from the user (based on simple geometries). Kriging goes beyond estimation to provide a model of uncertainty that is useful in determining how well understood estimation values are. Often kriging results are very smoothed. This can be aleviated by the use of heterogenous secondary data (see below) to better inform the kriging model about local variations. In addition, simulation models provide full access to point and joint uncertainty assessments and also produce more heterogeous maps the attribute (contaminant) of interest.

The following shows some typical applications of SADA geospatial models. In the first image we see an evaluation of correlation structure by creating a variogram map (rose) in search of anisotropic conditions and then the fitting of a model through experimental variogram results. The user has some assistance in this often challenging aspect of a geostatistical analysis with recommendations, autofitting, etc.

One product of a geospatial analysis is the contour map.

The local estimates of uncertainty in kriging (and simulation) translate into uncertainties about the final decision. In the following area of concern map, the exact boundary of the problem area is unknown and characterized by the green zone surrounding the gray (contaminated) zone. The think black line represents the best estimated boundary line given the current state of information and callibration of the model.

These bands of uncertainty serve as a jumping off point for discussion and implementation of secondary sampling designs that seek to optimally locate samples to better inform a particular decision or improve local geographical information.

In many situations, there is insufficient data to reasonably build a geospatial model of any kind. Maps of these types of geospatial models are very, very smooth.

Kriging these results produces the following map.

This is not to imply that such maps have no value. In fact, for many environmental characterizations there may never be more samples than the number found here and the state of information is limited by the availability of data. In some cases however, secondary information may be readily available. This secondary information is not per se a measurement of the attribute or contaminant of interest. However, there may exist a correlation between this secondary form of information and the primary information at hand. Examples of secondary data types include radiological walk over surveys, borehole scans, XRF, geological models, traditional geophysical measurements of the subsurface, and many other types of field detection methods. This information may be less exensive to collect and therefore more abundant.

This information can be explicitly used in the model to better inform them model, produce more heterogeneous maps, and reduce model/decision uncertainty. The following image shows the addition of a adding a densely collected geophysical survey to the analysis.

SADA Main Page Free Downloads Visualization Sampling Data Exploration Risk Assessment Geospatial Analysis Geospatial Simulation Decision Analysis Cost Benefit Anaylsis MARSSIM TRIAD Other Tools Technical Support Documentation Coming Soon Training Education Applications Join SADA User Group RAIS Bugs People Email Us

© Spatial Analysis and Decision Assistance Copyright 1996 University of Tennessee Research Corporation. All Rights Reserved.
© SADA Home Page Copyright 2007 University of Tennessee Research Corporation. All Rights Reserved.